Если радиус стержня больше десятой части длины волны, в уравнении для перемещения необходимо учитывать радиальные изменения. Тогда выражение для резонансной частоты принимает вид:

п

(5.8)

5.2.1.2. Стержневой резонатор с волной кручения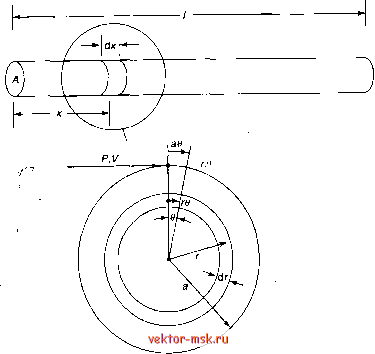

Рис. 5.4. Резонатор с волной кручения. Репродукция из книги R.A. John-.,; . , son, 1983, Mechanical Filters in Electronics, Wiley Interscience, New

York, с разрешения Wiley, ©1983 Wiley

На-рис. 5.4 показана схема возникновения волны кручения в стержне. Уравнение волны в этом случае совпадает с уравнением продольной волны. Угловое перемещение и резонансная частота имеют следующий вид:

в = во cos

ппх

(5.9)

п

д. 1/2

(5.10)

eq\r,l = ТГ/э/а'* 4г^ COS {~Г')

5.2.1.3. Стержневой резонатор с волной изгиба Схема возникновения волны изгиба в стержневом резонаторе показана на рис. 5.5. Уравнение имеет вид:

д'и рА д'и

(5.12)

где I - изгибающий момент инерции, котоы1И (ля прямоугольного стержня шириной w и толщиной h равен:

а для круглого стержня радиуса а -

(5.13)

(5.14)

2а

Рис. 5.5. Волна изгиба в стержневом резонаторе. Репродукция из книги R.A. Johnson, 1983, Mechanical Filters in Electronics, Wiley Interscience, New York с разрешения Wiley, ©1983 Wiley

Если оба конца стержня свободны или, наоборот, закреплены, уравнение для частоты находится из выражения:

cos kl =--

(5.15)

cosh kl

Корни этого уравнения равны: кц = 4.73, K2i = 7.853, К31 = 10.996, К41 = 14.137, ....

Дисперсионная зависимость между константой распространения волны и частотой имеет вид:

1.4 Р^, ,2

(5.16)

где G - модуль кручения, - угловое перемещение на конце стержня. Выражение для эквивалентной массы записывается как:

(5.11)

Отсюда находится выражение для резонансной частоты волны изгиба:

ikjffEiy (5.17)

(5Л8)

27Г/2 \рА

Уравнение для эквивалентной массы имеет следующий вид:

п -1

5.2.1.4- Резонат,оры с изгибающимся диском На рис. 5.6 показана схема возникновения волны изгиба в дисковом резонаторе. Ее уравнение в прямоугольных координатах имеет вид:

1 д^и

+ -+ 2-

(5.19)

Это уравнение проще всего решать в цилиндрической системе координат:

и{г, в) = [AJnikr) + BInikr)] cos пв. (5.20)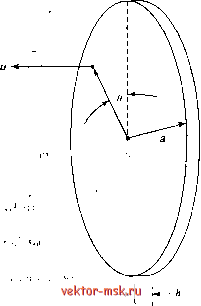

Рис. 5.6. Волна изгиба в диске. Репродукция из книги R.A. Johnson, 1983, Mechanical Filters in Electronics, Wiley Interscience, New York с разрешения Wiley, ©1983 Wiley

5.2. Моделирование механических фильтров 347 Найденное выражение для частоты можно записать как:

Jo(A:a) 1о{ка Ji{ka) Ii{ka)

= 0.

Дисперсионная зависимость в данном случае имеет вид:

Отсюда находится выражение для резонансной частоты:

Е

fs-{ka)l- L3p(l-/i2)J

(5.21)

(5.22)

(5.23)

Здесь индекс s соответствует центральной волне с круговой поляризацией изгибных колебаний. Уравнение для перемещения имеет вид:

h{kr)g

u{r)s = А

h{kr) -

Mkr),

-Jo (-{ka)s)

(5.24)

При s = 1 эквивалентная масса определяется выражением:

,1-2

= 0.2A7Mst

atic

u{r)

L (o)J

(5.25)

5.2.1.5. Толст,ые диски и пластины Дифференциальное уравнение, соответствующее колебаниям толстой круглой пластины, записывается как:

ph д^и

+ - + 2,

(5.26)

где р - плотность материала, h - толщина пластины, & D - ее диаметр.

Дисперсионная зависимость имеет вид:

а резонансная частота задается выражением:

(5.27)

(5.28)

348 Глава 5. Высокочастотные микрофильтры

Здесь а„ - корни характеристического уравнения (а„ = к^а): Jo{ka)Io{ka) - 1о{ка)4{ка) = 0.

Перемещение определяется как:

Jo (an).

(5.29)

(5.30)

5.2.1.6. Круговые и прямоугольные мембраны Для круговой мембраны радиуса а двумерное уравнение распространения волны в полярных координатах с началом координат в центре мембраны имеет вид:

&\ 1ди 1 ди р д'и

9г2 гдг^ г'дф F 9*2

= 0,

(5.31)

где р - масса на единицу площади мембраны, F - напряжение на ее краях. Дисперсионное соотношение для этого случая записывается как:

к = ш\.

(5.32)

Решение дифференциального уравнения в пространстве имеет следующий вид:

и{г,ф) - AcosmфJm (~) )

(5.33)

где А - произвольная константа, a i,n - значения а при J i{aa) = О, удовлетворяющие граничным условиям. Тогда резонансная частота задается следующим выражением:

Jm,n - г, I

2тга \р J

(5.34)

Для первых пяти значений резонансной частоты волновые коэффициенты в уравнении (5.34) равны: aoi = 2.406, ао2 = 5.52, аоз = 8.654, ао4 = 11.792 и ао5 = 14.931.

При применении прямоугольной мембраны дифференциальное уравнение меняется. В декартовых координатах его решение имеет вид:

. . тпх . ппу и{х,у) = Asm-sin

(5.35)

5.2. Моделирование механических фильтров

где а и b - размеры мембраны в направлениях х ш у, А - константа, тип - положительные целые числа, которые не могут одновременно равняться нулю.

Резонансная частота определяется выражением:

fm,n - 2

(7) + (б)

(5.36)

5.2.2. Компоненты линий связи

При описании механических резонансных характеристик соединительных компонентов, таких как балки, струны и планки, используют те же выражения, что и для традиционных механических фильтров. Хотя микрокомпоненты не всегда ведут себя как элементы нормальных размеров, такой анализ помогает смоделировать поведение системы в целом. Для микрокомпонентов сначала стараются разработать эквивалентную модель, считая их идеальными линиями передач. Как упоминалось ранее, разработка электрических эквивалентных схем отдельных компонентов значительно облегчает разработку всего фильтра. Эквивалентные схемы разрабатываются при помощи электромеханических аналогий. Для определения резонансных характеристик используются уравнение распространения волны с соответствующими граничными условиями.

5.2.2.1. Электрические линии передач Для упрощения составления эквивалентной схемы отдельных микрокомпонентов кратко рассмотрим эквивалентную схему двухпроводной электрической линии передач, в которой нет никаких потерь. Значения распределенных компонентов, показаных на рис. 5.7, соответствуют единице длины линии. Уравнения тока и напряжения для линии передач, составленные по данной модели, можно найти во многих учебниках, посвященных анализу электрических цепей и основам электромагнетизма. Однако для того, чтобы грамотно составлять эквивалентные схемы микрокомпонентов полезно понимать физические принципы распределенных линий.

Магнитная проницаемость используемых металлов и влияние индуктивности на изменение фаз токов на разной глубине линии являются причинами появления в эквивалентной схеме элементов индуктивности L. Диэлектрическая проницаемость среды между проводниками и геометрия линии отражаются в емкостных элементах С. Потери в проводниках и диэлектриках могут быть учтены в дополнительных компонентах проводимости G. Аналогично этому в