Ka Kz

coi 0} wp cob oji

S2i Sli

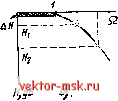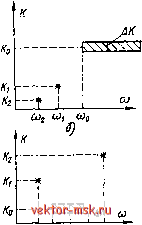coj ojn ojp ojb 0)i

Рис. 4.2. К вопросу о переходе от требований к ФНЧ (а), ФВЧ (б), ПФ (в) и РФ (г) к низкочастотному прототипу (д)

Для узкополосных фильтров (Q>1) справедливы следующие приближенные соотношения:

0)р - Шн Шв - Мр

В соответствии с (4.1) относительные частоты режекторного фильтра определяются аналогично полосовому, считая (Он и Шв на рис. 4.2г границами полосы режекции, тогда величины (Ор, Qu Q2, Q будут определяться аналогично предыдущему случаю.

Для ФНЧ, ФВЧ и ПФ Яl = 20Ig тг . W2=201g гг ; для РФ Я,=201д- ;

Л2 Аа Ло

2=201g . Ао

Аппроксимация. После определения требований к низкочастотному прототипу необходимо выбрать вид аппроксимации. Чаще других используются аппроксимации по Чебышеву или Баттерворту. Фильтр, описываемый полиномом Чебышева, имеет лучший коэффициент прямоугольности, т. е. используя его, можно обеспечить то же затухание на заданных частотах при меньшем числе звеньев. Преимуществом фильтра, описываемого полиномом Баттерворта, являются лучшее распределение неравномерности затухания в полосе пропускания и более равномерная фазовая характеристика, которая легче корректируется. Лучшее распределение неравномерности в таком фильтре заключается в плавном увеличении неравномерности при увеличении расстройки.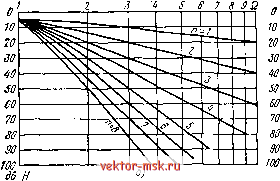

Рис. 4.3. Частотные характеристики фильтров при аппроксимации по Чебышеву при ЛЯ= 1 дБ (а) и по Баттерворту (б)

Для определения порядка полинома по требованиям к низкочастотному прототипу необходимо воспользоваться графиками затуханий, приведенных в [28-30]. При аппроксимации по Чебышеву графики даны для различных значений затухания в полосе пропускания АН (рис. 4.3а). Заметим, что при аппроксимации по Баттерворту затухание на частоте среза равно 3 дБ. На рис. 4.36 кривые затухания соответствуют полиному Баттерворта. После того как выбран вид аппроксимации, необходимо найти порядок полинома (я) так, чтобы кривая затухания на рис. 4.2 проходила ниже точек с нормированными частотами Qi, Й2 (рис. 4.2д}.

Таким образом будет определен порядок фильтра, являющегося низкочастотным прототипом требуемого фильтра.

Коэффициенты полиномов 2-го и 1-го порядка звеньев низкочастотного прототипа. Обычно вместе с графиками для полиномов различных порядков приводятся коэффициенты множителей 2-го и 1-го порядков. Так, для полиномов Че-бышева при ДЯ=1 дБ коэффициенты множителей представлены в табл. 4.1. Соответствующие коэффициенты множителей для полиномов Баттерворта даны в табл. 4.2.

Таблица 4.1

Порядок полинома

Множители 2-го и 1-го порядков и их коэффициенты, составляющие полином при аппроксимации по Чебышеву при неравномерности в полосе пропускания А Н = I дБ

3 4 5 6 7

0,907р2--0,996р-)-1

(1,006р2 -1-0,497р-1-1) (2,024р -1-1)

(1,014р2-ь0,283p-t-1) (3,579р2-Ь2,411 р-И)

(1,012р2+0,181 р -f-1) (2,330р2 -f 1,091 р -И) (3,454р -И)

(1,009р2 -Ь 0,126р4-1) (1,793р2 -f 0,609р-)-1) (8,019p2 -f 3,722р -t-1)

(1,007р2+0,092р -t-1) (1,530р2 -Ь 0,392р -1-1) (4,340р2 -Ь1,606р +1) X

,X(4,869p--!l)

(1,006р2+0,070р -Н1) (1,382р2+0,276р -1-1) (2,934р2 + 0,875р -h 1) X ,X(i4,232p2-b5,010p-f 1)

Пусть для какого-то фильтра задана чебышевская аппроксимация при ДЯ=11 дБ и оказалось, что требованиям к низкочастотному прототипу удовлетворяет полином 4-го порядка. Это означает, что низкочастотный прототип должен состоять из двух звеньев 2-го порядка с передаточными функциями

= 1 ши i . п OQO . . И Яра =

1.014р --0,283р-}- 1

3,579p?-f-2,411p.J-l

Таблица 4.2

Порядок полинома

Множители 2-го и 1-го порядков и их коэффициенты, составляющие полином при аппроксимации по Баттерворту

(р2+о,765р 4-1) (р2 +1,848рЧ-1)

(р--1)(р2+о,618р-Ц)(рН 1,618р+1)

(р2--0,518р+1) (р2-Ы,412р4-1) (р2+ l,932p-f 1)

(Р +1) {р'+0,445р-1--1) (р2-Ы,247р--1) (p2-f 1,802р--1)

(p2-)-0,390p-f 1) (р2-Ы,11 lp-1-1) (рН 1,166р-1-1) (рН 1,962р--1)

Переход от звеньев низкочастотного прототипа к звеньям требуемого фильтра. После того как получены передаточные функции звеньев низкочастотного прототипа, необходимо перейти к звеньям требуемого фильтра, используя следующие поистановкн:

для ФНЧ р = s/coq ,

для ФВЧ p = coo/s,

для ПФ р = Q [(wp/s) + (s/(Bp)],

для РФ

Q [(Wp/S) + (s/COp)]

На практике коэффициенты передаточных функций удобнее рассчитывать для относительных частот, где сйо=1 или а)р = 1, переходя к абсолютным частотам на последнем этапе - при расчете емкостей конденсаторов. В этом случае переход к звеньям требуемого фпльтра осуществляется подстановками

для ФНЧ

для ФВЧ для ПФ

для- РФ

p = s, p=l/s.

\ S /

(4.2)

После подстановки знаменатель передаточной функции требуемого звена представим в виде s-l-aQiS-l-fli. Здесь Qi - нормированная частота среза или нормированная резонансная частота t-ro звена. Если Qi = l, значит частоты среза или резонансные частоты i-ro звена и всего фильтра совпадают; а - величина, обратная добротности звена.

Пусть полученное в предыдущем примере первое звено требуется преобразовать в звено ФВЧ, тогда получим

1 s

i/(s)=-

1,014- + 0,283- +1 s

s? + 0,28Ы,007.s+ (1,007)2

Таким образом, в нашем случае = 0,281, Q, = 1,007.

Это означает, что добротность звена 1/а равна 3,56, а частота среза отличается ст частоты среза всего фильтра в 1,007 раз.